|
Blender
|
Python
Script:
Mesh
Manipulation,
(Part
5): Manufacturing Potatoids.
|
|
Version
Française
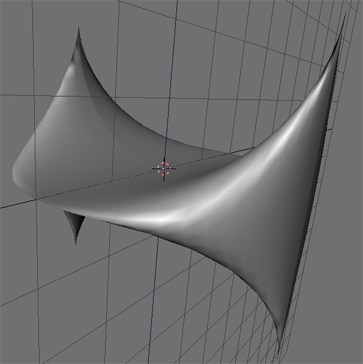
This slim and distinguished form is none
other than a "Potatoid". I.e. a volume derived from the equation of a sphere.
Its creation is not especially difficult, just utilize the block
concerning the creation of vertex co-ordinates in the previous examples.
...
for i in range(0, n):
for
j in range(0, n):
v=NMesh.Vert( i, j, 0 )
me.verts.append(v)
... |
We have just assigned the value of i
to
the co-ordinate X, and the value of j to Y. A variable is
added
for the radius, and three other variables : x, y, and z ; in which we will
store the result of the formulas. The following modifications make it possible
to obtain a true sphere. |
 |
...
# radius of the sphere
radius=2.0
for i in range(0, n):
for
j in range(0, n):
x = sin(j*pi*2/(n-1))*cos(-pi/2+i*pi/(n-1))*radius
y = cos(j*pi*2/(n-1))*cos(-pi/2+i*pi/(n-1))*radius
z = sin(-pi/2+i*pi/(n-1))*radius
v=NMesh.Vert(
x , y , z )
me.verts.append(v)
... |
 The previously presented form is obtained
by a very slight modification to the calculation of y
The previously presented form is obtained
by a very slight modification to the calculation of y
...
x=
sin(j*pi*2/(n-1))*cos(-pi/2+i*pi/(n-1))*radius
y=
cos(j*pi*2/(n-1)) * (1 -cos(-pi/2+i*pi/(n-1))
)
*
radius
z=
sin(-pi/2+i*pi/(n-1))*radius
... |
The gate is now opened for more experiments
and discoveries.
To obtain the file potatoid.py
The great potatoids
contest of the Little French's Tutorials
During all the 2000's summer, for the
greatest glory of Blender and the python, you are cordially invite to take
part in the most incredible potatoid's contest . Let send your propositions,
no picture!!, only the formula script, to:
jmsoler@free.fr
|
| Concurents |
formule |
Image |
| Timmy |
"mangled shell"
x=2*(1-2.718**((0.589*i)/(6*pi)))*cos(0.589*i)*(cos(0.5*0.196*j))**2
y= 2*(-1+2.718**((0.589*i)/(6*pi)))*cos(0.5*0.196*j)*cos(0.5*0.196*j)*sin(0.589*i)
z=1-2.718**((0.589*i)/(3*pi))-sin(0.916*j)+2.718**((0.589*i)/(6*pi))*sin(0.196*j)
Make
a display of the script
|
 |
| Une espèce de "Split Sea
Shell"
x=2*(1-e**((0.5236*i)/(6*pi)))*cos(0.5236*i)*(cos(0.5*0.1745*j))**2
y=2*(-1+e**((0.5236*i)/(6*pi)))*cos(0.5*0.1745*j)*cos(0.5*0.1745*j)*sin(0.5236*i)
z=1-e**((0.5236*i)/(3*pi))-sin(0.1745*j)
+ e**((0.5236*i)/(6*pi))*sin(0.1745*j)
Make
a display of the script |
 |
| thething |
s1=sin(j*pi*2/(n-1))
c2=cos(-pi/2+i*pi/(n-1))
c1=cos(j*pi*2/(n-1))
s2=sin(-pi/2+i*pi/(n-1)) |
| "good pillow"
x=s1*c2*2
y=c1*c2*2*0.5
z=s2*c1*2
Make
a display of the script |
 |
| "mulder's nightmare"
x=s1*c2*2
y=c1*c2*2
z=s2*c1*s1*2
Make
a display of the script |
 |
| "mulder's dream"
x=s1*c2*2
y=c1*c2*2
z=s2*c1*s1*2
Make
a display of the script |
 |
| "mulder's dream variation"
x=s1*c2*2
y=c1*c2*2
z=s2*c1*s1*2
Make
a display of the script |
 |
| "sexy saddle"
x=s1*c2*2
y=c1*c2*2
z=s2*c1*s1*2
Make
a display of the script |
 |
| "mechanical flower"
x=s1*c2*2
y=c1*c2*2
z=s2*c1*s1*2
Make
a display of the script |
 |
| "the lone star"
x=s1*c2*2
y=c1*c2*2
z=s2*c1*s1*2
Make
a display of the script |
 |
| . |
| jö |
"noeud de trèfle"
Not exactly a potatoid, but the contruction
of the mesh is, quite, identical.
Afficher
le script |
 |
|

